
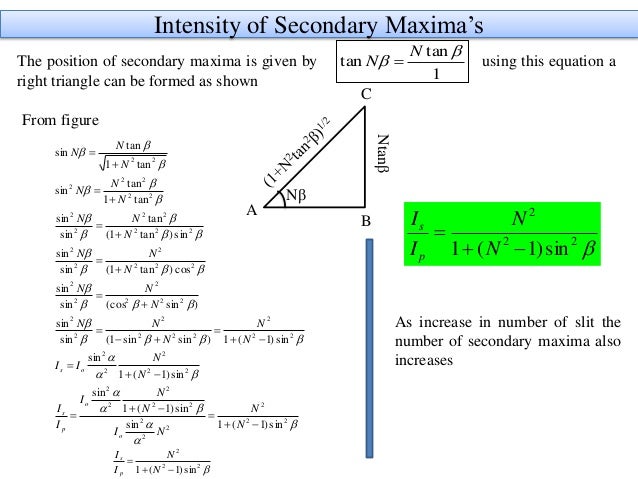
Where, dλ is the difference in wavelength between two spectral lines of equal intensity. Resolving “power” is a theoretical concept and is given by: 3 shows a “flat field” spectrograph as used with a linear diode array. In a spectrograph, the linear dispersion for any wavelength other than the wavelength which is normal to the spectral plane will be modified by the cosine of the angle of inclination or tilt angle (γ) at wavelength λ n. Linear dispersion, therefore, varies directly with cos β, and inversely with the exit path length, L B, diffraction order (k), and groove density, n. In a monochromator, L B is the arm length from the focusing mirror to the exit slit, or if the grating is concave, from the grating to the exit slit. Where L B is the effective exit focal length in mm and dx is the unit interval in mm along the focal field (see Fig.

Linear dispersion perpendicular to the diffracted beam at a central wavelength, λ, is given by: Linear dispersion is associated with an instrument’s ability to resolve fine spectral detail. The second instrument demonstrates “low” dispersion compared to the “higher” dispersion of the first. It is easy to imagine that fine spectral detail would be more easily identified in the first instrument than the second.
For example, consider two spectrometers: one instrument disperses a 0.1 nm spectral segment over 1 mm while the other takes a 10 nm spectral segment and spreads it over 1 mm. 6.Linear dispersion defines the extent to which a spectral interval is spread out across the focal field of a spectrometer and is expressed in nm/mm, Å/mm, cm -1/mm, etc. The arrows on the gratings indicate the blaze direction and the relationship between the groove profile and this direction is shown in Fig. The blaze wavelengths given for concave gratings in catalog are the blaze wavelengths for the configuration (mounting) in the optical system used. In this case, then, select a grating for which λ B(Litt) = 500 nm from the catalog. It can be seen from this equation that, when not using the Littrow configuration, the blaze wavelength λ B is shorter than λ B(Litt).įor incident angle α, the relationship between λ B(Litt) and λ B is given by the following:įor example, for a groove density N of 600 grooves/mm and an incident angle α of 60°, in order to obtain first-order light with a wavelength of 300 nm, substiture λ B = 300 nm in equation (13) to obtain λ B(Litt) = 484 nm. The relationship between the blaze wavelength λ B for other configurations and the blaze wavelength λ B(Litt)used in the catalog is given by the following: Equation (12) is Substituted equation (11) for equation (10) and applied m to both sides.

In our catalogs, the blaze wavelengths given for plane gratings are the blaze wavelengths for this configuration. In this case, α = β = θ B then equation (8) gives the following: In gerneral, the wavelength (λ B(Litt)) where first-order diffracted light returns along the same path as the incident light is used to represent the blaze characteristics of gratings. It can be seen from this equation that the blaze wavelength varies with the blaze angle θ B and the incident angle α (i.e., the usage method). Combining equations (8) and (9) gives the following: The corresponding wavelength is called the "blaze wavelength" and is represented by λ B.


 0 kommentar(er)
0 kommentar(er)
